Datenfiles und R-Code zu Beispielen aus der LVA finden Sie auch auf der TUWEL-Seite zur Lehrveranstaltung.
Wie in den Unterlagen zur Lehrveranstaltung vezeichnet \(S\) den Preis des Basiswerts und \(K\) den Ausübungspreis.
Welchen Portfoliogewinn / -verlust haben Sie am 21.03.2025 mit bzw. ohne Sicherung, falls der Preis von GE Aerospace an diesem Tag
Laut Tabelle in den LVA Unterlagen ist der Briefkurs (Ask-Preis) am 7.1.2025 bei $5.00. Die Kosten für den Kauf des Portfolios sind $17,200.00 für die Aktien und $250.00 für die eventuelle Teilsicherung. Macht Gesamtkosten von $17,200.00 ohne Teilsicherung und $17,450.00 inklusive Teilsicherung.
Angenommen am 07.01.2025 besitzt eine Investorin eine Aktie GE Aerospace und schreibt auf diese Aktie einen Call mit Verfallstag 21.03.2025 und einem Ausübungspreis von $190.
Was ist der niedrigste Preis zu dem der Händler die Call Option anbieten kann, um noch einen positiven Payoff zu generieren?
Zahlung zum Verfallstag
Beispiel: Abhängigkeit vom Preis des Basiswerts
Am Verfallstag der Option: Welche der folgenden Positionen profitieren zum Verfallstag von einem höheren Preis des Basiswerts, wenn die Option zum Verfallstag im Geld ist?- Long-Position in einer Kaufoption.
- Long-Position in einer Verkaufsoption .
- Short-Position in einer Kaufoption.
- Short-Position in einer Verkaufsoption.
Wie in den Unterlagen zur Lehrveranstaltung vezeichnet \(S\) den Preis des Basiswerts und \(K\) den Ausübungspreis.
- Der Wert einer Kaufoption ist zum Fälligkeitstag gleich
\(C_T=\max\{S_T-K,0\}\)
Die Option ist im Geld, das bedeutet für eine Kaufoption \(S_T>K\), daher profitiert der Wert der Kaufoption von einem höheren \(S_T\). - Der Wert einer Verkaufsoption ist zum Fälligkeitstag gleich
\(P_T=\max\{K-S_T,0\}\)
Die Option ist im Geld, das bedeutet für eine Verkaufsoption \(S_T < K\), daher leidet der Wert der Verkaufsoption bei höherem \(S_T\). - Da der Wert der Kaufoption mit dem Preis des Basiswerts steigt, sinkt der Wert der Short-Position in einer Kaufoption mit \(S_T\).
- Da der Wert der Verkaufsoption mit dem Preis des Basiswerts sinkt, profitiert der Wert der Short-Position in einer Verkaufsoption mit \(S_T\).
Portfoliosicherung zum Verfallstag
Beispiel: GE Aerospace
Sie Kaufen am 07.01.2025 100 Stück Aktien von GE Aerospace zum Preis von $172.00/Stück. Außerdem überlegen Sie, Ihr Portfolio teilweise gegen Wertverlust durch den Kauf von 50 Stück Put Optionen mit dem Verfallstag 21.03.2025 und einem Ausübungspreis von 160 abzusichern. Wie in den LVA-Unterlagen angeführt, zahlt GE Aerospace die nächste Dividende am 11.04.2025.Welchen Portfoliogewinn / -verlust haben Sie am 21.03.2025 mit bzw. ohne Sicherung, falls der Preis von GE Aerospace an diesem Tag
- $180.00 beträgt?
- $170.00 beträgt?
- $160.00 beträgt?
- $150.00 beträgt?
Laut Tabelle in den LVA Unterlagen ist der Briefkurs (Ask-Preis) am 7.1.2025 bei $5.00. Die Kosten für den Kauf des Portfolios sind $17,200.00 für die Aktien und $250.00 für die eventuelle Teilsicherung. Macht Gesamtkosten von $17,200.00 ohne Teilsicherung und $17,450.00 inklusive Teilsicherung.
- Bei einem Aktienkurs von $180 ist die Aktienposition $18,000.00 wert. Die Put Optionen verfallen aus dem Geld und sind
daher wertlos,
\(50 P_T = 50 \max\{K-S_T,0\} = 50 \max\{160-180,0\}=0,\)
daher ist der Wert des Portfolios gleich $18,000.00. Der Porfoliogewinn ist mit Sicherung $550.00, ohne Sicherung $800.00. - Bei einem Aktienkurs von $170 ist die Aktienposition $17,000.00 wert. Die Put Optionen verfallen aus dem Geld und sind
daher wertlos,
\(50 P_T = 50 \max\{K-S_T,0\} = 50 \max\{160-170,0\}=0,\)
daher ist der Wert des Portfolios gleich $17,000.00. Der Portfolioverlust ist mit Sicherung $450.00, ohne Sicherung $200.00. - Bei einem Aktienkurs von $160 ist die Aktienposition $16,000.00 wert. Die Put Optionen verfallen aus dem Geld und sind
daher wertlos,
\(50 P_T = 50 \max\{K-S_T,0\} = 50 \max\{160-160,0\}=0,\)
daher ist der Wert des Portfolios gleich $16,000.00. Der Portfolioverlust ist mit Sicherung $1,450.00, ohne Sicherung $1,200.00. - Bei einem Aktienkurs von $150 ist die Aktienposition $15,000.00 wert. Die Put Optionen sind nun aber im Geld und haben
einen Wert von
\(50 P_T = 50 \max\{K-S_T,0\} = 50 \max\{160-150,0\}=500,\)
daher ist der Wert des gesicherten Portfolios gleich $15,500.00. Der Portfolioverlust ist mit Sicherung $1,950.00, ohne Sicherung $2,200.00.
Covered Call Writing
Beispiel: GE Aerospace
Eine bei Privatanlegern beliebte Strategie zur Generierung von Portfolio-Cashflow ist die sog. Covered Call Writing Strategie, bei der man einen Call auf eine Aktie schreibt, die man im Portfolio besitzt.Angenommen am 07.01.2025 besitzt eine Investorin eine Aktie GE Aerospace und schreibt auf diese Aktie einen Call mit Verfallstag 21.03.2025 und einem Ausübungspreis von $190.
- Eine Call Option auf eine Aktie zu schreiben (= eine Short-Position einzugehen), ist sehr riskant, weil man dabei ein unbeschränktes Verlustrisiko eingeht. Warum hat die Covered Call Strategie dieses Verlustpotential nicht, obwohl dabei eine Short-Position in einer Call Option enthalten ist?
- Wie sieht eine Gewinn- / Verlustrechnung am 21.03.2025 in Abhängigkeit vom dann realisierten Preis der GE Aerospace Aktie aus?
- Das Risiko der Short-Call Position wird mit der Aktie, die im Besitz der Stillhalterin ist, abgesichert. Wenn die Option ausgeübt wird, erhält die Investorin den Ausübungspreis von $190.00 und tritt die Aktie an die Gegenseite der Call Option ab. Damit ist deren Anspruch befriedigt -- unabhängig vom Aktienkurs.
- Laut Tabelle in den LVA Unterlagen ist der Schlusskurs der GE Aerospace Aktie am 07.01.2025 gleich $172.31.
Der Geldkurs (Bid-Preis) der Call Option ist $4.05. D.h., der Cashflow am 07.01.2025 ist gleich $4.05.
Die Gewinn- / Verlustrechnung der Covered Call Strategie \(\Delta_{CC}\) am Verfallstag der Option ist\(\begin{eqnarray*} \Delta_{CC} &=& S_T - \max\{0,S_T-K\} - (S_0-C_0) = C_0 + \min\{S_T-S_0, K-S_0\}\\ &=& 4.05 + \min\{S_T-172.31,190-172.31\} = 4.05 + \min\{S_T-172.31,17.96\}. \end{eqnarray*}\)
Dagegen ist der Gewinn / Verlust der reinen Aktienstrategie \(\Delta_{S}\) gleich\(\Delta_S = S_T-S_0\).
Die Covered Call Strategie bringt sofort die Zahlung der Call Prämie von $4.05. Im Gegenzug ist aber das Gewinnpotential Aktie beschränkt. Falls die Aktie über $190.00 steigt, wird der Call ausgeübt und die Aktie muss im Austausch gegen den Ausübungspreis abgegeben werden. Damit ist das Gewinnpotential der Aktie mit $17.96 beschränkt und der gesamte Gewinn mit 4.05+17.69 = 21.74.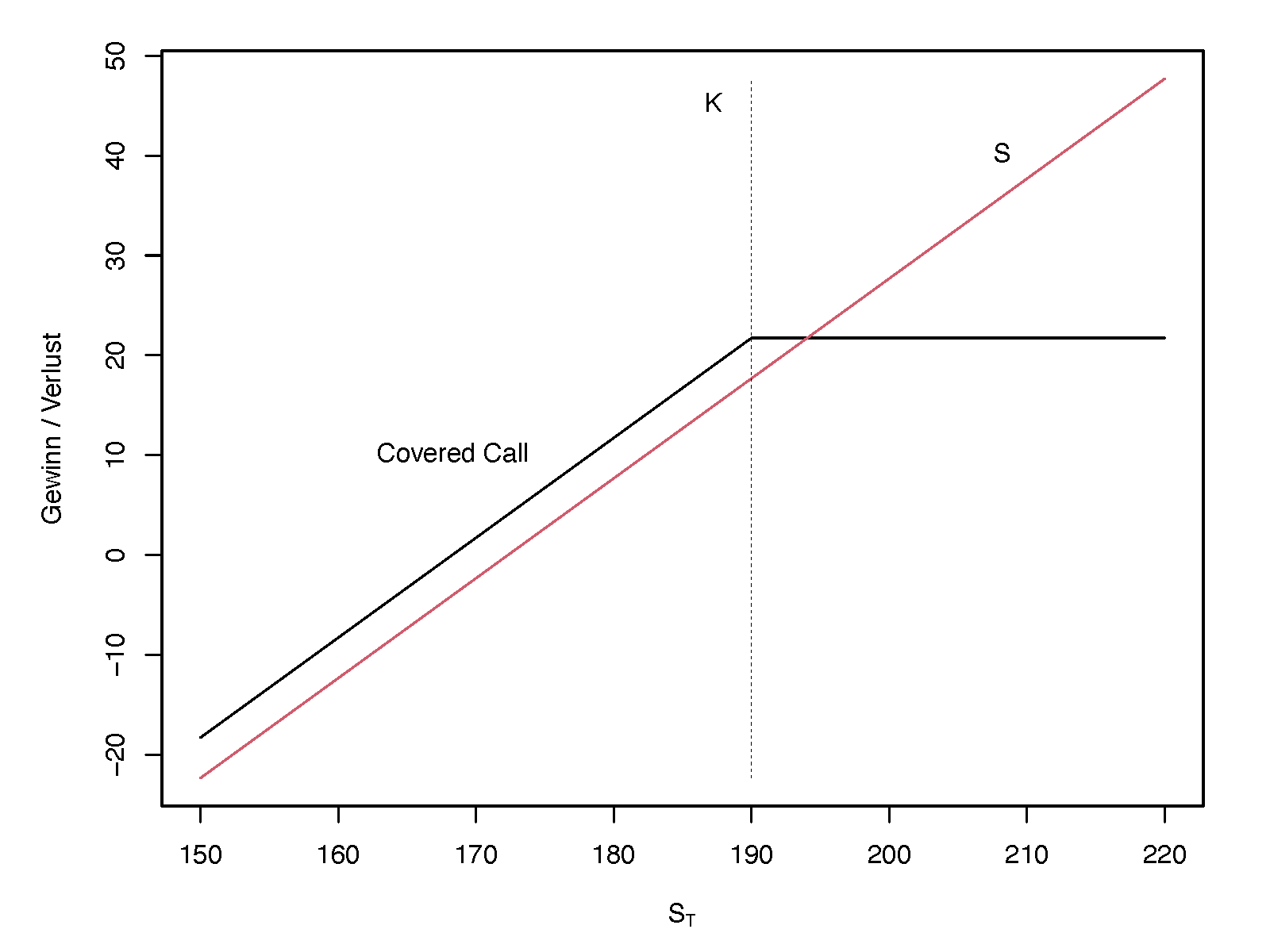
Put-Call-Parity
Put-Call-Parity
Ein Optionshändler handelt OTC (over the counter -- nicht öffentlich) mit Optionen. Eine Kundin ist interessiert am Kauf einer Europäischen Call Option auf Aktien der Firma XYZ interessiert, mit Laufzeit ein Jahr und Ausübungspreis $20.00. Ein anderer Kunde ist bereit eine Put Option auf XYZ zu schreiben, ebenfalls mit Laufzeit ein Jahr und Ausübungspreis $20.00. Dafür erwartet er einen Preis von $3.50. Die Aktie von XYZ handelt derzeit bei $18.00. Der risikolose Zinssatz ist 6% pro Jahr. XYZ zahlt keine Dividenden.Was ist der niedrigste Preis zu dem der Händler die Call Option anbieten kann, um noch einen positiven Payoff zu generieren?
- Der Optionshändler kann die Zahlungen der Call Option exakt durch ein Portfolio aus dem Put, der Aktie und
einer risikolosen Veranlagung replizieren und sich damit vollständig absichern.
Wenn er also als Preis für die Call Option zumindest die Kosten für das replizierende Portfolio setzt, generiert er
zu \(t=0\) eine positive Zahlung und hat zu \(t=T\) keinerlei Verpflichtungen--weil abgesichert.
\(C = P + S - \text{PV}(K) = 3.50 + 18.00 - \Frac{20}{1.06} = 2.632\)