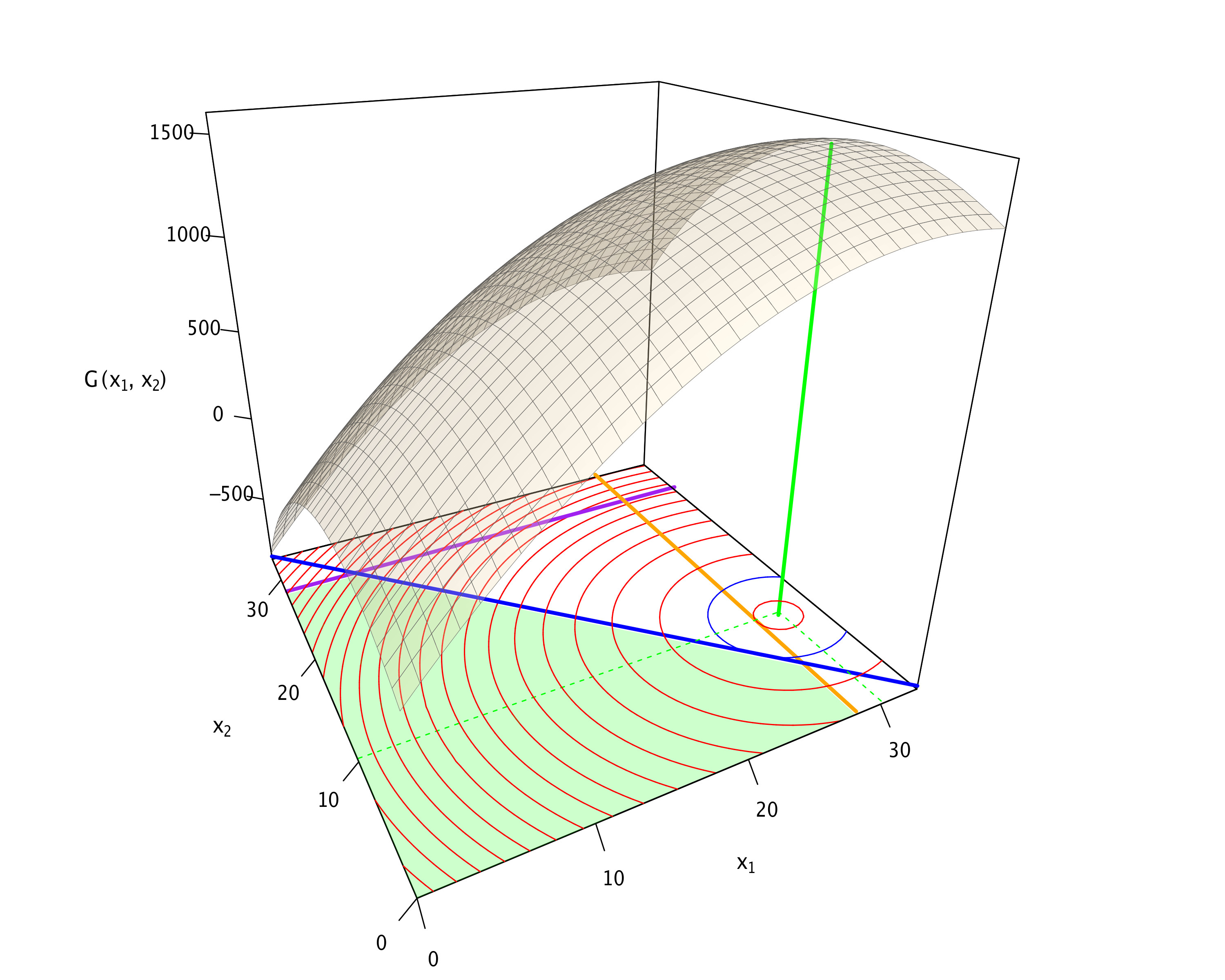
Die unbeschränkte Lösung
- Der erste Versuch ist immer die Lösung des unbeschränkten Problems. D.h., bei diesem ersten Lösungsansatz sind alle Lagrange-Multiplikatoren (Schattenpreise) gleich 0, \(\lambda_1=0\), \(\lambda_2=0\), \(\lambda_3=0\). Mit dieser Festlegung sind die Complementary Slackness-Bedingungen (3), (6), (9) jedenfalls erfüllt. Die Nebenbedingungen (1), (4), (7) sind daher nicht notwendigerweise bindend und sind daher drei Ungleichungen, die von einer Lösung des Gleichungssystems erfüllt werden müssen.
Außerdem nehmen wir in diesem ersten Lösungsversuch an, dass die Produktionsmengen einer internen Lösung entspringen, d.h., dass die relativen Deckungsbeiträge (10) und (13) gleich 0 sind. Als Ungleichungen, die von der Lösung erfüllt werden müssen, bleiben (11) und (14), also \(x_1\geq 0\), \(x_2\geq 0\). - Die getroffenen Annahmen machen nun das ursprüngliche System von Ungleichungen zu einem lösbaren Gleichungssystem. Die Gleichungen (2'), (5'), (8'), (10') und (13') sind fünf Gleichungen, welche die fünf Variablen des Problems eindeutig festlegen.
- Die ermittelte Lösung des Gleichungssystems muss auch die fünf Ungleichungen (1), (4), (7), (11) und (14) erfüllen, nur dann ist sie ein echter Kandidat für ein Maximum.
- Die Lösung dieses Gleichungssystems ist
- Diese Lösung lässt sich auch durch Wahl von \(\lambda_1=0\), \(\lambda_2=0\), \(\lambda_3=0\) auf der interaktiven Lösungsseite ermitteln: Interaktive Lösung.
- Diese Lösung verletzt aber die Nebenbedingungen 1 und 2, wie auch aus der Graphik zu sehen ist. Bitte beachten: Da alle \(\lambda\) gleich 0 sind, ist die Lagrange-Funktion gleich der Gewinn-Funktion.
- Hier geht's zurück zur schrittweisen Lösung des Produktionsproblems, wo weitere Schritte zur Lösung des Problems diskutiert werden.
Die Kuhn-Tucker Bedingungen lauten unter diesen Annahmen
\(\begin{array}{rclcrcll} (1)&&\Frac{\partial L}{\partial \lambda_1}(\lambda^*,x^*)&=&33-x_1^*-x_2^*&\geq&0,&\mbox{(NB)}\\ (2')&&&&\lambda_1^*&=&0,&\mbox{(Schattenpreis)}\\[1em] (4)&&\Frac{\partial L}{\partial \lambda_2}(\lambda^*,x^*)&=&28-x_1^*&\geq&0,&\mbox{(NB)}\\ (5')&&&&\lambda_2^*&=&0,&\mbox{(Schattenpreis)}\\[1em] (7)&&\Frac{\partial L}{\partial \lambda_3}(\lambda^*,x^*)&=&28-x_2^*&\geq&0,&\mbox{(NB)}\\ (8')&&&&\lambda_3^*&=&0,&\mbox{(Schattenpreis)}\\[1em] (10')&&\Frac{\partial L}{\partial x_1}(\lambda^*,x^*)&=&90-3x_1^*-\lambda_1^*-\lambda_2^*&=&0,&\mbox{(rel. DB)}\\ (11)&&&&x_1^*&\geq&0,&\mbox{(Variable)}\\[1em] (13')&&\Frac{\partial L}{\partial x_2}(\lambda^*,x^*)&=&40-4x_2^*-\lambda_1^*-\lambda_3^*&=&0,&\mbox{(rel. DB)}\\ (14)&&&&x_2^*&\geq&0,&\mbox{(Variable)}\\ \end{array}\)
\(\begin{array}{rclrclrcl} \lambda_1&=&0,&\lambda_2&=&0,&\lambda_3&=&0,\\ x_1&=&30,&x_2&=&10. \end{array}\)