Beispiel 3
Bearbeitung des Punktes a) aus gegebenem Produktionsproblem:
- Bestimme die optimale Produktionsentscheidung \(x_1\) und \(x_2\), welche den Gesamtgewinn des Unternehmens maximiert.
- Zielfunktion = Gesamtgewinn. In jeder der Perioden errechnet sich der Gewinn aus Erlös minus Produktionskosten, Fixkosten sind in dem Beispiel keine zu berücksichtigen, weil nicht angegeben:
- Wenn das Unternehmen in der ersten Periode \(x_1\) Einheiten produziert und absetzt, dann ist der Gewinn in dieser Periode
\(\begin{array}{rcl} G_1(x_1)&=&p_1x_1-10 x_1\\ &=&(100-1.5x_1)x_1-10x_1\\ &=&90x_1-1.5x_1^2 \end{array}\)
- In der zweiten Periode macht das Unternehmen bei Produktion und Absatz von \(x_2\) Einheiten einen Gewinn von
\(\begin{array}{rcl} G_2(x_2)&=&p_2x_2-10 x_2\\ &=&(50-2x_2)x_2-10x_2\\ &=&40x_2-2x_2^2 \end{array}\)
\(G(x_1,x_2)=G_1(x_1)+\frac{1}{1+r}G_2(x_2),\)
wobei \(r\) die adäquate Diskontrate ist. In unserem einfachen Beispiel ist der Zeitwert des Geldes allerdings mit 0 angenommen, d.h., \(r=0\), und daher haben wir als Zielfunktion des Unternehmens
\(\begin{array}{rcl} G(x_1,x_2)&=&G_1(x_1)+G_2(x_2)\\ &=&(100-1.5x_1)x_1-10x_1 + (50-2x_2)x_2-10x_2\\ &=&90x_1-1.5x_1^2+ 40x_2-2x_2^2\to_{x_1,x_2}\max \end{array}\)
- Wenn das Unternehmen in der ersten Periode \(x_1\) Einheiten produziert und absetzt, dann ist der Gewinn in dieser Periode
- Nebenbedingungen. Bei der Gewinnmaximierung müssen folgende Nebenbedingungen eingehalten werden:
- Gesamtproduktion darf 33 Einheiten nicht übersteigen:
- Die Produktion in der ersten Periode darf 28 Einheiten nicht übersteigen:
- Die Produktion in der zweiten Periode darf 28 Einheiten nicht übersteigen:
\(g^1: x_1+x_2\leq 33\quad\Rightarrow\quad g^1(x_1,x_2)=33-x_1-x_2\geq 0\)
\(g^2: x_1\leq 28\quad\Rightarrow\quad g^2(x_1,x_2)=28-x_1\geq 0\)
\(g^3: x_2\leq 28\quad\Rightarrow\quad g^3(x_1,x_2)=28-x_2\geq 0\)
- 3D-Darstellung der Gewinnfunktion. Die folgende Abbildung zeigt die Gewinnfunktion des Unternehmens in Abhängigkeit von den gewählten Produktionsmengen \(x_1\) und \(x_2\) gemeinsam mit den Nebenbedingungen (genauer: dem bindenden Rand der Nebenbedingungen). In Blau der bindende Rand \(g^1=0\), in Orange \(g^2=0\) und in Violet \(g^3=0\). Der grüne Bereich ist der zulässige Bereich.
- Das unbeschränkte Maximum der Zielfunktion liegt nicht im zulässigen Bereich. Wie wir weiter unten sehen werden, liegt das unbeschränkte Maximum bei \(x_1=30\), \(x_2=10\) und verletzt damit sowohl die Bedingung \(g^1\) als auch die Bedingung \(g^2\).
- Unter keinen Umständen können alle drei Nebenbedingungen gleichzeitig bindend sein.
- Das Optimierungsziel ist es, mit einer zulässigen Lösung ein möglichst hohes Gewinn-Niveau zu erreichen. In der Abbildung sieht man, dass die höchste, zulässig erreichbare Isoquante die in Blau eingezeichnete ist. Das ist jene, die den zulässigen Bereich gerade berührt.
- Nun aber zur systematischen Lösung des Problems mit Hilfe des Kuhn-Tucker-Formalismus
- Lagrange-Funktion. Die Lagrange-Funktion des Problems lautet
- Kuhn-Tucker-Bedingungen. Ist ein Punkt \((\lambda^*,x^*)=(\lambda_1^*,\lambda_2^*,\lambda_3^*,x_1^*,x_2^*)\) eine optimale Lösung des Produktionsproblems, dann müssen folgende Bedingungen erfüllt sein.
- Ungleichung (1) ist die erste Nebenbedingung, Ungleichung (2) ist die Vorzeichenrestriktion für den zugehörigen Schattenpreis \(\lambda_1^*\). Die Complementary Slackness-Bedingung (3) stellt den Zusammenhang her: Wenn die linke Seite von (1) echt größer als 0 ist (d.h., die Nebenbedingung ist nicht bindend), dann muss der zugehörige Schattenpreis \(\lambda_1^*\) gleich 0 sein, denn ansonsten ist (3) verletzt.
Umgekehrt kann der Schattenpreis nur dann ungleich 0 sein, wenn die Nebenbedingung bindend ist! Welcher der beiden Fälle nun zutrifft, ist nicht von vornherein klar und muss getestet werden. - Die (Un-) Gleichungen (4), (5) und (6) stellen das entsprechende System von (Un-) Gleichungen rund um die zweite Nebenbedingung und ihren Schattenpreis dar. Die (Un-) Gleichungen (7), (8) und (9) das System zur dritten Nebenbedingung.
- Ungleichung (11) gibt an, dass die Produktionsmengen nicht negativ sein dürfen. Die linke Seite der Ungleichung (10) stellt den relativen Deckungsbeitrag einer (marginalen) zusätzlich produzierten Einheit in der ersten Periode, auch relativer Grenz-Deckungsbeitrag genannt, dar. Würde man \(x_1^*\) um \(dx_1^*\) erhöhen, dann ändert sich der Gewinn gemäß Grenzgewinn, d.h., entlang der partiellen Ableitung der Gewinnfunktion um den Betrag \((90-3x_1^*)dx_1^*\). Gleichzeitig erhöht sich aber auch der Ressourcenverbrauch (Verbrauch der zur Verfügung stehenden Einheiten Gesamtproduktion und der Einheiten Produktion in der ersten Periode). Der Wert dieses zusätzlichen Verbrauchs ist \((\lambda_1^*+\lambda_2^*)dx_1^*\) und muss vom Grenzgewinn abgezogen werden, um den relativen, marginalen Deckungsbeitrag oder relativen Grenz-Deckungsbeitrag zu erhalten.
Die Complementary Slackness-Bedingung (12) verbindet die Ungleichungen (10) und (11). Wird in der Periode 1 produziert, \(x_1^*>0\), dann muss der relative Grenz-Deckungsbeitrag gleich 0 sein, denn sonst kann die gewählte Produktionsmenge \(x_1^*\) nicht optimal gewählt sein. Wenn in der Periode 1 nicht produziert wird, \(x_1^*=0\), dann kann der relative Grenz-Deckungsbeitrag echt negativ sein. Denn der besagt dann, dass jede produzierte Einheit den Lösungswert verschlechtern würde, deshalb ist in diesem Fall \(x_1^*=0\) optimal. - Das System (13), (14) und (15) verbindet Produktionsmenge und relativen Grenz-Deckungsbeitrag in der 2. Periode.
Außerdem ist das Maximum der Gewinnfunktion durch die grüne, vertikale Linie eingezeichnet, gemeinsam mit einer Schar von Isoquanten der Gewinnfunktion.
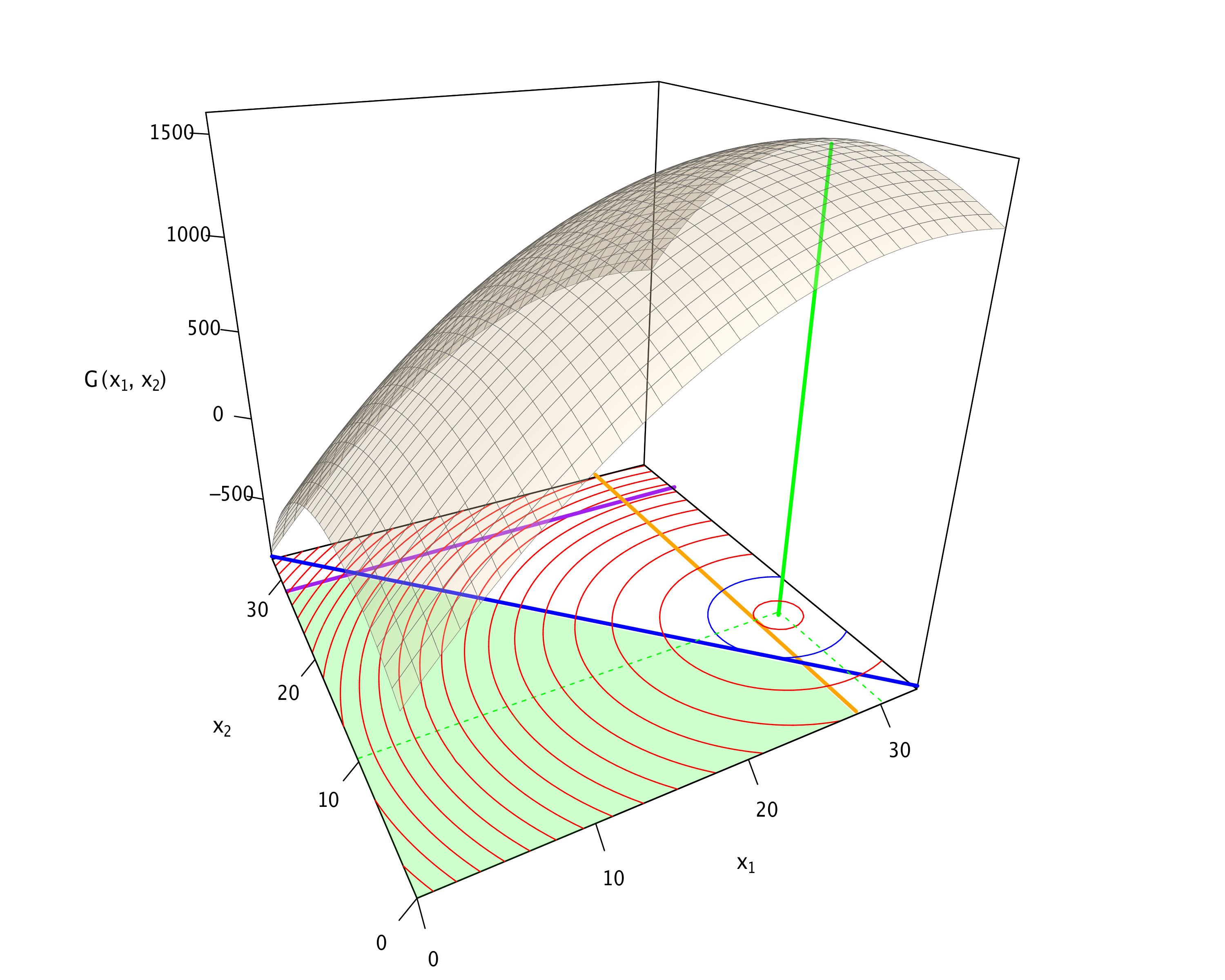
Folgende Beobachtungen lassen sich anhand der Abbildung machen:
\(\begin{array}{rcl} L(\lambda_1,\lambda_2,\lambda_3,x_1,x_2)&=&G(x_1,x_2)\\ &&+\lambda_1 g^1(x_1,x_2)\\ &&+\lambda_2 g^2(x_1,x_2)\\ &&+\lambda_3 g^3(x_1,x_2)\\ &=&90x_1-1.5x_1^2+ 40x_2-2x_2^2\\ &&+\lambda_1 (33-x_1-x_2)\\ &&+\lambda_2 (28-x_1)\\ &&+\lambda_3 (28-x_2). \end{array}\)
\(\begin{array}{rclcrcll} (1)&&\Frac{\partial L}{\partial \lambda_1}(\lambda^*,x^*)&=&33-x_1^*-x_2^*&\geq&0,&\mbox{(NB)}\\ (2)&&&&\lambda_1^*&\geq&0,&\mbox{(Schattenpreis)}\\ (3)&&\Frac{\partial L}{\partial \lambda_1}(\lambda^*,x^*)\lambda_1^*&=&(33-x_1^*-x_2^*)\lambda_1^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (4)&&\Frac{\partial L}{\partial \lambda_2}(\lambda^*,x^*)&=&28-x_1^*&\geq&0,&\mbox{(NB)}\\ (5)&&&&\lambda_2^*&\geq&0,&\mbox{(Schattenpreis)}\\ (6)&&\Frac{\partial L}{\partial \lambda_2}(\lambda^*,x^*)\lambda_2^*&=&(28-x_1^*)\lambda_2^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (7)&&\Frac{\partial L}{\partial \lambda_3}(\lambda^*,x^*)&=&28-x_2^*&\geq&0,&\mbox{(NB)}\\ (8)&&&&\lambda_3^*&\geq&0,&\mbox{(Schattenpreis)}\\ (9)&&\Frac{\partial L}{\partial \lambda_3}(\lambda^*,x^*)\lambda_3^*&=&(28-x_2^*)\lambda_3^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (10)&&\Frac{\partial L}{\partial x_1}(\lambda^*,x^*)&=&90-3x_1^*-\lambda_1^*-\lambda_2^*&\leq&0,&\mbox{(rel. DB)}\\ (11)&&&&x_1^*&\geq&0,&\mbox{(Variable)}\\ (12)&&\Frac{\partial L}{\partial x_1}(\lambda^*,x^*)x_1^*&=&(90-3x_1^*-\lambda_1^*-\lambda_2^*)x_1^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (13)&&\Frac{\partial L}{\partial x_2}(\lambda^*,x^*)&=&40-4x_2^*-\lambda_1^*-\lambda_3^*&\leq&0,&\mbox{(rel. DB)}\\ (14)&&&&x_2^*&\geq&0,&\mbox{(Variable)}\\ (15)&&\Frac{\partial L}{\partial x_2}(\lambda^*,x^*)x_2^*&=&(40-4x_2^*-\lambda_1^*-\lambda_3^*)x_2^*&=&0.&\mbox{(Comp. Slack.)} \end{array}\)
Jeweils drei (Un-) Gleichungen stehen in direkter Relation zueinander (durch Absätze gekennzeichnet).
Die Möglichkeit zur interaktiven Lösung des Problems durch geeignete Wahl der Lagrange-Multiplikatoren finden Sie hier: Interaktive Lösung. Je nach Wahl der Multiplikatoren werden die Kuhn-Tucker-Bedingungen ausgewertet und die Lagrange-Funktion dargestellt.
Lösungsschritte
- Was macht es nun schwierig, dieses System von (Un-) Gleichungen zu lösen?
- Jeweils zwei der Ungleichungen sind durch eine Complementary Slackness-Bedingung miteinander verknüpft. Diese stellt sicher, dass immer zumindest eine der beiden Ungleichungen bindend ist, d.h., dass die Bedingung \(=0\) lautet.
- Im Fall der Nebenbedingungen: Entweder die Nebenbedingung bindet, oder der zugehörige Lagrange-Multiplikator ist gleich 0 (oder beides).
- Im Fall der Variablen: Entweder der relative Deckungsbeitrag einer Variable ist gleich 0 oder die Variable selbst ist gleich 0 (oder beides).
- Es ist also ein kombinatorisches Problem: Bei \(m\) Nebenbedingungen und \(n\) Variablen gibt es \(2^{(n+m)}\) verschiedene Möglichkeiten.
- Für jede mögliche Festlegung (Nebenbedingung bindend oder nicht, Variable positiv oder gleich 0), erhält man aus jeder der obigen Dreiergruppen von (Un-) Gleichungen je eine Gleichung und eine Ungleichung.
- Also insgesamt ein System von \(m+n\) Gleichungen in \(m+n\) Variablen UND ein System von \(m+n\) Ungleichungen. Nur wenn die Lösung des Gleichungssystems auch alle Ungleichungen erfüllt, sind die Bedingungen erster Ordnung (die Kuhn-Tucker Bedingungen) erfüllt.
- Der erste Versuch ist immer die Lösung des unbeschränkten Problems. D.h., bei diesem ersten Lösungsansatz sind alle Lagrange-Multiplikatoren (Schattenpreise) gleich 0, \(\lambda_1=0\), \(\lambda_2=0\), \(\lambda_3=0\).
Dadurch ist die Lagrange-Funktion gleich der ursprünglichen Gewinn-Funktion. - Eine genauere Diskussion der unbeschränkten Lösung finden Sie hier: Unbeschränkte Lösung
- Die unbeschränkte Lösung \(\lambda_1=0\), \(\lambda_2=0\), \(\lambda_3=0\), \(x_1=30\), \(x_2=10\) verletzt aber die Nebenbedingungen 1 und 2 und kann daher keine Lösung des Gesamtproblems sein!
- Da bei der unbeschränkten Lösung die Nebenbedingungen 1 und 2 verletzt sind, nehmen wir nun an, dass diese beiden Bedingungen bindend sind. D.h., \(\lambda_1>0\), \(\lambda_2>0\), \(\lambda_3=0\).
Bemerkung: In welcher Reihenfolge man die unterschiedlichen Möglichkeiten auswählt, ist durch die Kuhn-Tucker Methode nicht vorgegeben. - Eine genauere Diskussion der Lösung bei bindenden Nebenbedingungen 1 und 2 finden Sie hier: Nebenbedingung 1 und 2 bindend
- Die unter diesen Annahmen ermittelte Lösung ist
\(\begin{array}{rclrclrcl} \lambda_1&=&20,&\lambda_2&=&-14,&\lambda_3&=&0,\\ x_1&=&28,&x_2&=&5. \end{array}\)
Das ist aber keine Lösung des Gesamtproblems, weil der Lagrange Multiplikator der zweiten Nebenbedingung negativ ist (für eine genauere Diskussion siehe oben angeführten Link). - Da in obigem Fall die Nebenbedingung 2 einen Lagrange Multiplikator mit falschem Vorzeichen hatte, nehmen wir nun an, dass nur Nebenbedingung 1 bindend ist, \(\lambda_1>0\), \(\lambda_2=0\), \(\lambda_3=0\)
- Eine genauere Diskussion der Lösung bei bindender Nebenbedingung 1 finden Sie hier: Nebenbedingung 1 bindend
- Damit ist nun die Lösung des Produktionsproblems gefunden (alle Kuhn-Tucker Bedingungen sind erfüllt, die hinreichenden Optimalitätsbedingungen für ein Maximum sind erfüllt, kein weiterer Punkt erfüllt die Kuhn-Tucker Bedingungen, das unbeschränkte Problem ist nach oben beschränkt):
\(\begin{array}{rclrclrcl} \lambda_1&=&12,&\lambda_2&=&0,&\lambda_3&=&0,\\ x_1&=&26,&x_2&=&7. \end{array}\)