Nebenbedingung 1 bindend
- Wir ermitteln nun die Lösung unter der Annahme, dass nur Nebenbedingung 1 bindet, \(g^1=0\). D.h., die Complementary-Slackness Bedingung zu dieser Nebenbedingung ist jedenfalls erfüllt, auch wenn der zugehörige Schattenpreis ungleich 0 ist, \(\lambda_1\geq 0\).
- Die Nebenbedingungen 2 und 3 sind weiterhin nicht bindend, d.h., \(\lambda_2=0\), \(\lambda_3=0\) und die zugehörigen Nebenbedingungen (4) und (7) bleiben \(\geq 0\) Ungleichungen.
- Die getroffenen Annahmen führen wieder dazu, dass jede Dreier-(Un-) Gleichungsgruppe des Kuhn-Tucker Systems eine Gleichung und eine Ungleichung entsendet. Das System der Gleichungen liefert eine Lösung, die aber auch das System der Ungleichungen erfüllen muss. Nur dann ist der ermittelte Punkt auch ein Kandidat für eine Gesamtlösung.
- Die Lösung des Gleichungssystems (1'), (5'), (8'), (10'), (13') ist
- Diese Lösung lässt sich auch durch Wahl von \(\lambda_1=12\), \(\lambda_2=0\), \(\lambda_3=0\) auf der interaktiven Lösungsseite ermitteln: Interaktive Lösung.
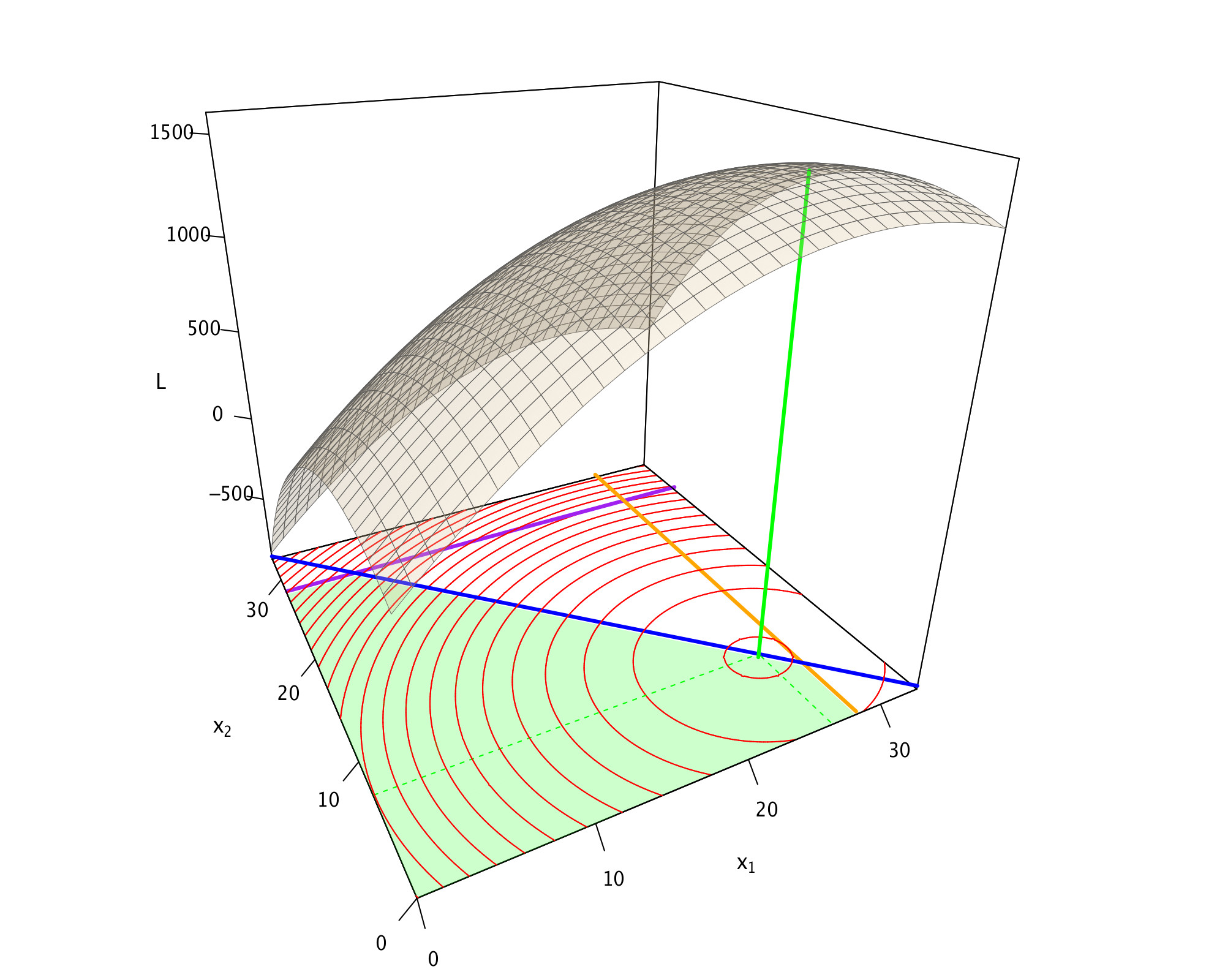
- Diese Lösung des Gleichungssystems (1'), (5'), (8'), (10'), (13') ist nun in Übereinstimmung mit den Ungleichungen (2), (4), (7), (11), (14)!
- Der Lagrange Multiplikator der bindenden Nebenbedingung 1 ist positiv. Die beiden anderen Nebenbedingungen sind nicht verletzt. Und beide Produktionsmengen sind positiv.
- Wir haben also einen Kandidaten für ein Maximum gefunden. Wenn das Lagrange Problem, welches sich aus der Zielfunktion und der Nebenbedingung 1 ergibt, die hinreichenden Optimalitätsbedingungen für ein Maximum erfüllt, haben wir ein lokales Maximum des Gesamtproblems gefunden.
- Nachdem die hinreichenden Bedingungen erfüllt sind, kein weiterer Kandidat für ein Maximum gefunden werden kann und die Zielfunktion nach oben beschränkt ist (mit dem unbeschränkten Maximum), ist die gefundene Lösung das globale Maximum des Produktionsproblems!
- Hier geht's zurück zur schrittweisen Lösung des Produktionsproblems, wo weitere Schritte zur Lösung des Problems diskutiert werden.
Die Annahmen bezüglich \(x_1\) und \(x_2\) bleiben so wie im Fall der unbeschränkten Lösung. \(x_1\geq 0\), \(x_2\geq 0\) und (10) und (13) sind daher Gleichungen \(= 0 \).
Die Kuhn-Tucker Bedingungen lauten unter diesen Annahmen
\(\begin{array}{rclcrcll} (1')&&\Frac{\partial L}{\partial \lambda_1}(\lambda^*,x^*)&=&33-x_1^*-x_2^*&=&0,&\mbox{(NB)}\\ (2)&&&&\lambda_1^*&\geq&0,&\mbox{(Schattenpreis)}\\[1em] (4)&&\Frac{\partial L}{\partial \lambda_2}(\lambda^*,x^*)&=&28-x_1^*&\geq&0,&\mbox{(NB)}\\ (5')&&&&\lambda_2^*&=&0,&\mbox{(Schattenpreis)}\\ (7)&&\Frac{\partial L}{\partial \lambda_3}(\lambda^*,x^*)&=&28-x_2^*&\geq&0,&\mbox{(NB)}\\ (8')&&&&\lambda_3^*&=&0,&\mbox{(Schattenpreis)}\\[1em] (10')&&\Frac{\partial L}{\partial x_1}(\lambda^*,x^*)&=&90-3x_1^*-\lambda_1^*-\lambda_2^*&=&0,&\mbox{(rel. DB)}\\ (11)&&&&x_1^*&\geq&0,&\mbox{(Variable)}\\[1em] (13')&&\Frac{\partial L}{\partial x_2}(\lambda^*,x^*)&=&40-4x_2^*-\lambda_1^*-\lambda_3^*&=&0,&\mbox{(rel. DB)}\\ (14)&&&&x_2^*&\geq&0,&\mbox{(Variable)}\\ \end{array}\)
\(\begin{array}{rclrclrcl} \lambda_1&=&12,&\lambda_2&=&0,&\lambda_3&=&0,\\ x_1&=&26,&x_2&=&7. \end{array}\)