Beispiel 3
Bearbeitung des Punktes c) aus gegebenem Produktionsproblem:
- Angenommen, die Emissionsbeschränkung wird aufgehoben. Stattdessen wird eine Emissionssteuer von EUR 12 pro produzierter Einheit eingehoben. Was ist nun die optimale Produktionsentscheidung?1
- Zielfunktion = Gesamtgewinn. Im Vergleich zu den vorigen Beispielen erhöhen sich nun die variablen Kosten um EUR 12 pro Einheit:
- Wenn das Unternehmen in der ersten Periode \(x_1\) Einheiten produziert und absetzt, dann ist der Gewinn in dieser Periode
\(\begin{array}{rcl} G_1(x_1)&=&p_1x_1-(10 + 12)x_1\\ &=&(100-1.5x_1)x_1-22x_1\\ &=&78x_1-1.5x_1^2 \end{array}\)
- In der zweiten Periode macht das Unternehmen bei Produktion und Absatz von \(x_2\) Einheiten einen Gewinn von
\(\begin{array}{rcl} G_2(x_2)&=&p_2x_2-(10 + 12) x_2\\ &=&(50-2x_2)x_2-22x_2\\ &=&28x_2-2x_2^2 \end{array}\)
\(\begin{array}{rcl} G(x_1,x_2)&=&G_1(x_1)+G_2(x_2)\\ &=&(100-1.5x_1)x_1-22x_1 + (50-2x_2)x_2-22x_2\\ &=&78x_1-1.5x_1^2+ 28x_2-2x_2^2\to_{x_1,x_2}\max \end{array}\)
- Wenn das Unternehmen in der ersten Periode \(x_1\) Einheiten produziert und absetzt, dann ist der Gewinn in dieser Periode
- Nebenbedingungen. Bei der Gewinnmaximierung müssen folgende Nebenbedingungen eingehalten werden:
Gesamtproduktion darf 33 Einheiten nicht übersteigen:Menge wird nun durch Steuer verringert!- Die Produktion in der ersten Periode darf 28 Einheiten nicht übersteigen:
- Die Produktion in der zweiten Periode darf 28 Einheiten nicht übersteigen:
\(g^1: x_1\leq 28\quad\Rightarrow\quad g^1(x_1,x_2)=28-x_1\geq 0\)
\(g^2: x_2\leq 28\quad\Rightarrow\quad g^2(x_1,x_2)=28-x_2\geq 0\)
- 3D-Darstellung der Gewinnfunktion. Die folgende Abbildung zeigt die Gewinnfunktion des Unternehmens in Abhängigkeit von den gewählten Produktionsmengen \(x_1\) und \(x_2\).
Im Vergleich zur Gewinnfunktion aus dem ursprünglichen Beispiel führt die Emissionssteuer von EUR 12 pro erzeugter Einheit nun zu einer flacheren Gewinnfunktion. Die Abgabe entspricht genau dem ermittelten Schattenpreis für die Emissions-Nebenbedingung (\(x_1 + x_2 <= 33\)).
Darüber hinaus sind die Nebenbedingungen skizziert (genauer: deren bindender Rand). Strichliert in blauer Farbe der bindende Rand, der nun nicht mehr vorhandenen Emissions-Nebenbedingung \(33 - x_1 - x_2 >= 0\), in Orange \(g^1=0\) und in Violett \(g^2=0\). Der grüne Bereich ist der zulässige Bereich. - Das unbeschränkte Maximum der Zielfunktion liegt nun im zulässigen Bereich und zwar im Punkt (26, 7). Diese Produktionsentscheidung entspricht exakt jener des ursprünglichen Problems mit Emissionsbeschränkung! Der Ersatz der Beschränkung durch die Emissionsabgabe in Höhe des zugehörigen Schattenpreises implementiert exakt dieselbe Lösung wie die Anwendung der Nebenbedingung (daher die Bezeichnung Schattenpreis der Nebenbedingung). In diesem Punkt sind alle Nebenbedingungen erfüllt.
- Nun aber zur systematischen Lösung des Problems mit Hilfe des Kuhn-Tucker-Formalismus
- Lagrange-Funktion. Die Lagrange-Funktion des Problems lautet
- Kuhn-Tucker-Bedingungen. Ist ein Punkt \((\lambda^*,x^*)=(\lambda_1^*,\lambda_2^*,x_1^*,x_2^*)\) eine optimale Lösung des Produktionsproblems, dann müssen folgende Bedingungen erfüllt sein.
- Wie in der Grafik zu sehen, ist dieses Gleichungssystem leicht zu lösen und man kommt bereits mit der unbeschränkten Lösung auf das gesuchte Ergebnis.
- Zur Lösung des unbeschränkten Problems setzen wir alle Lagrange-Multiplikatoren (Schattenpreise) gleich 0, \(\lambda_1=0\), \(\lambda_2=0\).
Dadurch ist die Lagrange-Funktion gleich der ursprünglichen Gewinn-Funktion. - Eine genauere Diskussion der unbeschränkten Lösung des ursprünglichen Problems finden Sie hier: Unbeschränkte Lösung
- Die unbeschränkte Lösung \(\lambda_1=0\), \(\lambda_2=0\), \(x_1=26\), \(x_2=7\) verletzt keine der Nebenbedingungen und ist somit Lösung des Gesamtproblems! Da die unbeschränkte Lösung immer den bestmöglichen Kandidaten für ein Maximum gibt, ist die gefundene Lösung das globale Maximum des Produktionsproblems (alle Kuhn-Tucker Bedingungen und die hinreichenden Optimalitätsbedingungen für ein Maximum sind erfüllt)!
Daran wird ersichtlich, dass die explizite Einschränkung der Menge über die Emissionsbedingung \(x_1 + x_2 <= 33\) und zusätzliche Stückkosten in der Höhe des Schattenpreises (Lagrange-Multiplikator) äquivalent sind (vergleiche Beispiel a).
Außerdem ist das Maximum der Gewinnfunktion durch die grüne, vertikale Linie eingezeichnet.
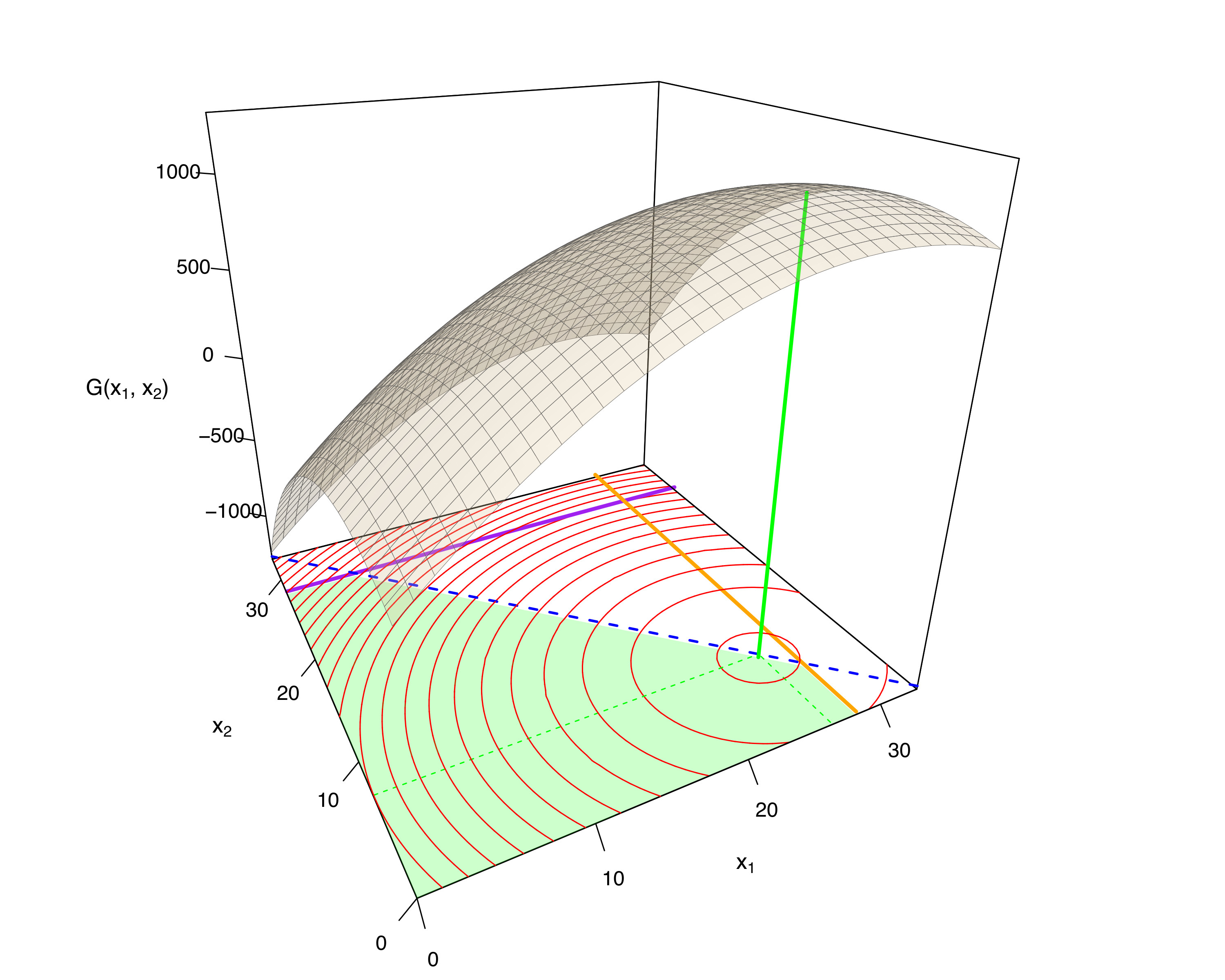
Folgende Beobachtungen lassen sich anhand der Abbildung machen:
\(\begin{array}{rcl} L(\lambda_1,\lambda_2,x_1,x_2)&=&G(x_1,x_2)\\ &&+\lambda_1 g^1(x_1,x_2)\\ &&+\lambda_2 g^2(x_1,x_2)\\ &=&78x_1-1.5x_1^2+ 28x_2-2x_2^2\\ &&+\lambda_1 (28-x_1)\\ &&+\lambda_2 (28-x_2)\\ \end{array}\)
\(\begin{array}{rclcrcll} (1)&&\Frac{\partial L}{\partial \lambda_1}(\lambda^*,x^*)&=&28-x_1^*&\geq&0,&\mbox{(NB)}\\ (2)&&&&\lambda_2^*&\geq&0,&\mbox{(Schattenpreis)}\\ (3)&&\Frac{\partial L}{\partial \lambda_1}(\lambda^*,x^*)\lambda_1^*&=&(28-x_1^*)\lambda_2^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (4)&&\Frac{\partial L}{\partial \lambda_2}(\lambda^*,x^*)&=&28-x_2^*&\geq&0,&\mbox{(NB)}\\ (5)&&&&\lambda_3^*&\geq&0,&\mbox{(Schattenpreis)}\\ (6)&&\Frac{\partial L}{\partial \lambda_2}(\lambda^*,x^*)\lambda_2^*&=&(28-x_2^*)\lambda_3^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (7)&&\Frac{\partial L}{\partial x_1}(\lambda^*,x^*)&=&78-3x_1^*-\lambda_1^*-\lambda_2^*&\leq&0,&\mbox{(rel. DB)}\\ (8)&&&&x_1^*&\geq&0,&\mbox{(Variable)}\\ (9)&&\Frac{\partial L}{\partial x_1}(\lambda^*,x^*)x_1^*&=&(78-3x_1^*-\lambda_1^*-\lambda_2^*)x_1^*&=&0,&\mbox{(Comp. Slack.)}\\[1em] (10)&&\Frac{\partial L}{\partial x_2}(\lambda^*,x^*)&=&28-4x_2^*-\lambda_1^*-\lambda_3^*&\leq&0,&\mbox{(rel. DB)}\\ (11)&&&&x_2^*&\geq&0,&\mbox{(Variable)}\\ (12)&&\Frac{\partial L}{\partial x_2}(\lambda^*,x^*)x_2^*&=&(28-4x_2^*-\lambda_1^*-\lambda_3^*)x_2^*&=&0.&\mbox{(Comp. Slack.)} \end{array}\)
Jeweils drei (Un-) Gleichungen stehen in direkter Relation zueinander (durch Absätze gekennzeichnet).
Lösungsschritte
Unbeschränkte Lösung
1 Herzlichen Dank an Herrn Fatjon Zogaj für die Unterstützung bei der Erstellung des Textes zu Punkt c des Beispiels.